Although an increasing number of RDF knowledge bases are published, many of those consist primarily of instance data and lack sophisticated schemata. Having such schemata allows more powerful querying, consistency checking and debugging as well as improved inference. One of the reasons why schemata are still rare is the effort required to create them. In this project, we propose a semi-automatic schemata construction approach addressing this problem: First, the frequency of terminological axiom patterns in existing knowledge bases is discovered. Afterwards, those patterns are converted to SPARQL based pattern detection algorithms, which allow to enrich knowledge base schemata. We argue that we present the first scalable knowledge base enrichment approach based on real schema usage patterns. The approach is evaluated on a large set of knowledge bases with a quantitative and qualitative result analysis.
As an example for knowledge base enrichment, consider an axiom pattern
A ≡ B ⊓ ∃r.C
which might be instantiated by an axiom
SoccerPlayer ≡ Person ⊓ ∃team.SoccerClub
describing that every person which is in a team that is a soccer club, is a soccer player.
Adding such an axiom to a knowledge base can have several benefits:
- The axioms serve as documentation for the purpose and correct usage of schema elements.
- They improve the application of constraint violation techniques. For instance, when using a tool such as the Pellet Constraint Validator on a knowledge base with the above axiom, it would report soccer players without an associated team as violation.
- Additional implicit information can be inferred, e.g. in the above example each person, who is in a soccer club team can be inferred to belong to the class Soccer Player, which means that an explicit assignment to that class is no longer necessary.
General Workflow
Execution Phase
In the execution phase the actual axiom suggestions are generated. To achieve this, a single algorithm run takes an axiom pattern and usually a specific class name as input and generates a set of OWL axioms
as a result. It proceeds in three phases:
- In the first phase, SPARQL queries are used to obtain general information about the knowledge base, in particular we retrieve axioms, which allow to construct the class hierarchy. It can be configured whether to use an OWL reasoner for inferencing over the schema or just taking explicit knowledge into account.(Naturally, the schema only needs to be obtained once per knowledge base and can then be reused by all algorithms and all entities.)
- The second phase consists of obtaining data via SPARQL, which is relevant for learning the considered axiom. This results in a set of axiom candidates, configured via a threshold.
- In the third phase, the score of axiom candidates is computed and the results returned.
Evaluation
Pattern Detection
The analysis of the following ontology repositories
| Repository | #Ontologies | #Axioms | ||||||||||||
| Total | Error | Total | Tbox | RBox | Abox | |||||||||
| Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | |||
| TONES | 214 | 12 | 0 | 14299 | 1235392 | 0 | 8297 | 658449 | 0 | 20 | 932 | 0 | 5981 | 1156468 |
| BioPortal | 385 | 101 | 0 | 25541 | 847755 | 0 | 23353 | 847755 | 0 | 35 | 1339 | 0 | 2152 | 220948 |
| Oxford | 793 | 0 | 0 | 49997 | 2492761 | 0 | 15384 | 2259770 | 0 | 25 | 1365 | 0 | 34587 | 2452737 |
This results in the following top 15 TBox axiom patterns occurring in at least 5 ontologies ranked by frequency. Each row contains the position/rank of the pattern in each repository. In addition, we also report the winsorised frequency: In the sorted list of pattern frequencies for each ontology (without 0-entries), we set all list entries higher than the 95th percentile to the 95th percentile. This reduces the effect of outliers, i.e. axiom patterns scoring very high because of few very large ontologies frequently using them
| Pattern | Frequency | Winsorized Frequency |
#Ontologies | TONES | BioPortal | Oxford | |
|---|---|---|---|---|---|---|---|
| 1. | A⊑B | 10,174,991 | 5,757,410 | 1050 | 2 | 1 | 1 |
| 2. | A⊑∃p.B | 8,199,457 | 2,450,582 | 604 | 1 | 2 | 2 |
| 3. | A⊑∃p.(∃q.B) | 509,963 | 441,434 | 24 | n/a | n/a | 3 |
| 4. | A≡B⊓∃p.C | 361,777 | 316,420 | 319 | 8 | 4 | 4 |
| 5. | B⊑¬A | 237,897 | 53,516 | 417 | 3 | 3 | 9 |
| 6. | A≡B | 104,443 | 8332 | 151 | 13 | 34 | 7 |
| 7. | A≡∃p.B | 70,040 | 11,031 | 139 | 36 | 32 | 8 |
| 8. | ∃p.Thing⊑A | 41,876 | 11,031 | 595 | 6 | 7 | 11 |
| 9. | A⊑∀p.B | 27,556 | 21,046 | 266 | 4 | 11 | 19 |
| 10. | A≡B⊓∃p.C⊓∃q.D | 24,277 | 20,277 | 196 | 11 | 13 | 13 |
| 11. | A≡B⊓C | 16,597 | 16,597 | 78 | 5 | 20 | 22 |
| 12. | A⊑∃p.(B⊓∃q.C) | 12,453 | 12,161 | 84 | 23 | 18 | 15 |
| 13. | A⊑∃p.{a} | 11,816 | 4342 | 65 | 12 | 22 | 20 |
| 14. | A≡B⊓∃p.(C⊓∃q.D) | 10,430 | 10,430 | 60 | 39 | 21 | 17 |
| 15. | p≡q- | 9943 | 7393 | 433 | 17 | 19 | 23 |
Table:
Top 15 TBox axiom patterns.
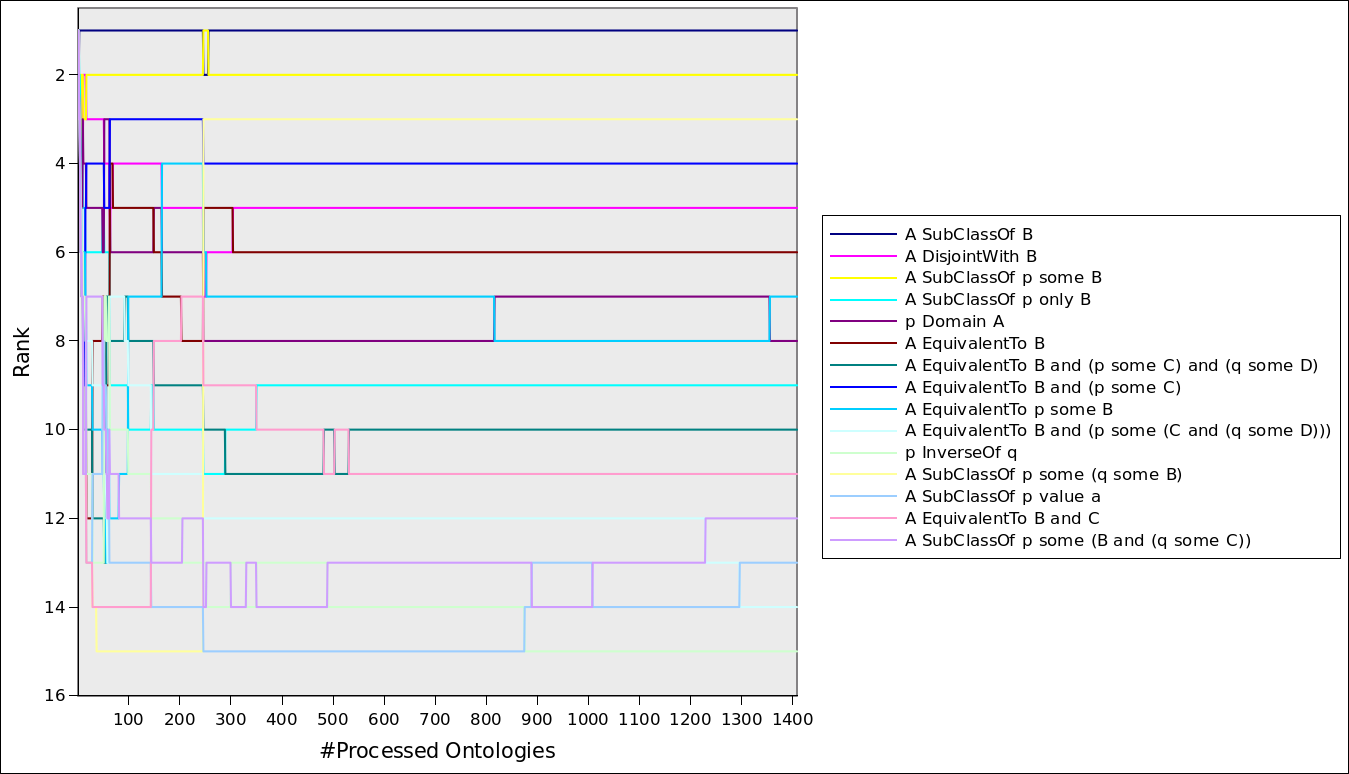
Fixpoint Analysis
Top 15 axiom patterns and its sequence of total frequency when processing the ontologies in random order:
Top 15 axiom patterns and its ranking position when processing the ontologies in random order:
Pattern Application
Experimental Setup
SPARQL Endpoint: http://live.dbpedia.org/sparql
Analyzed classes: 100 random classes with at least 5 instances
Max. time for fragment extraction: 60s
3 evaluators
Max. 100 instantiations per pattern with an accuracy < 0.6
Results
(The evaluation results are not final yet.)
Overall results:
| Pattern | #Axioms | Correct | Minor Issues | Incorrect |
|---|---|---|---|---|
| A SubClassOf p some B | 50 | 88.0 | 1.3 | 10.7 |
| A SubClassOf B | 47 | 63.8 | 2.1 | 34.0 |
| A EquivalentTo B | 25 | 10.7 | 0.0 | 89.3 |
| A EquivalentTo p some B | 68 | 29.9 | 2.0 | 68.1 |
| A EquivalentTo B and (p some C) | 100 | 25.0 | 3.0 | 72.0 |
| A EquivalentTo B and (p some (C and (q some D))) | 100 | 23.0 | 5.3 | 71.7 |
| A SubClassOf p some (q some B) | 71 | 86.4 | 3.3 | 10.3 |
| A SubClassOf p some (B and (q some C)) | 100 | 87.0 | 0.3 | 12.7 |
| A SubClassOf p value a | 15 | 77.8 | 0.0 | 22.2 |
| A EquivalentTo B and C | 42 | 14.3 | 7.1 | 78.6 |
| A EquivalentTo B and (p some C) and (q some D) | 100 | 38.0 | 2.7 | 59.7 |
| Total | 718 | 48.6 | 2.7 | 48.7 |
Inter-Rater Agreement(Fleiss’ Kappa) for each evaluated pattern:
| Pattern | #Axioms | Fleiss’ Kappa |
|---|---|---|
| A EquivalentTo p some B | 68 | 0.6 |
| A EquivalentTo B and (p some C) | 100 | 0.73 |
| A SubClassOf p some (B and (q some C)) | 100 | -0.03 |
| A SubClassOf B | 47 | 0.54 |
| A SubClassOf p some B | 50 | 0.19 |
| A EquivalentTo B | 25 | 0.44 |
| A SubClassOf p value a | 15 | 0.36 |
| A SubClassOf p some (q some B) | 71 | 0.4 |
| A EquivalentTo B and (p some C) and (q some D) | 100 | 0.8 |
| A EquivalentTo B and C | 42 | 0.47 |
| A EquivalentTo B and (p some (C and (q some D))) | 100 | 0.43 |
Total Inter-Rater Agreement: 0.67
Threshold Analysis
The following diagram shows the correlation between the accuracy value of the pattern instantiations and the confidence of the evaluators, i.e. how many of the pattern instantiations with an accuracy value in a particular interval are supposed to be correct.
To perform the analysis, question were added in 10% buckets by confidence interval (60–70%,<70%-80%,<80%-90%,<90%-100%). Only buckets with at least 5 entries were used (which is why the lines are interrupted). For most axiom types, the trend is that axioms with higher confidence are more likely to be accepted, although two of the 12 axiom types show a decline with higher confidence. We will investigate this further and also add an overall trend summary.